
Lesson 4: More Examples of Functions
Date:
12/18/13
45
© 2013 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
NYS COMMON CORE MATHEMATICS CURRICULUM
8•5
Lesson 4
Lesson 4: More Examples of Functions
Student Outcomes
Students examine and recognize real-world functions, such as the cost of a book, as discrete rates.
Students examine and recognize real-world functions, such as the temperature of a pot of cooling soup, as
continuous rates.
Classwork
Discussion (5 minutes)
In the last couple of lessons we looked at several linear functions and the numbers that are assigned by the
function in the form of a table.
Table A:
Bags of Candy
(
)
1
2
3
4
5
6
7
8
Cost
()
$1.25
$2.50
$3.75
$5
$6.25
$7.50
$8.75
$10
Table B:
Number of
Seconds
()
0.5
1
1.5
2
2.5
3
3.5
4
Distance
Traveled in Feet
()
4
16
36
64
100
144
196
256
In Table A, the context was purchasing bags of candy. In Table B, it was the distance traveled by a moving
object. Examine the tables. What are the differences between these two situations?
Provide time for students to discuss the differences between the two tables and share their thoughts with the class.
Then continue with the discussion below.
For the function in Table A, we said that the rule that described the function was = 1.25, where 0.
Why did we restrict to numbers equal to or greater than zero?
We restricted to numbers equal to or greater than zero because you cannot purchase 1 bags of
candy, for example.
If we assume that only a whole number of bags can be sold because a bag cannot be opened up and divided
into fractional parts, then we need to be more precise about our restriction on . Specifically, we must say that
is a positive integer, or 0. Now, it is clear that only 0, 1, 2, 3, etc. bags can be sold as opposed to 1.25
bags or 5.7 bags.
Lesson 4: More Examples of Functions
Date:
12/18/13
46
© 2013 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
NYS COMMON CORE MATHEMATICS CURRICULUM
8•5
Lesson 4
With respect to Table B, the rule that describes this function was = 16
. Does this problem require the
same restrictions on as the previous problem? Explain.
We should state that must be a positive number because represents the amount of time traveled,
but we do not need to say that must be a positive integer. The intervals of time do not need to be in
whole seconds; the distance can be measured at fractional parts of a second.
We describe these different rates as discrete and continuous. When only positive
integers make sense for the input of a function, like the bags of candy example,
we say that it is a discrete rate problem. When there are no gaps in the values of
the input, for example fractional values of time, we say that it is a continuous rate
problem. In terms of functions, we see the difference reflected in the input
values of the function. We cannot do problems of motion using the concept of
unit rate without discussing the meaning of constant speed.
Example 1 (6 minutes)
This is another example of a discrete rate problem.
Example 1
If copies of the same book cost $, what is the unit rate for the book?
The unit rate is
or dollars per book.
The total cost is a function of the number of books that are purchased. That is, if is the cost of a book and is
the total cost, then = 64.
What cost does the function assign to 3 books? 3.5 books?
For 3 books: = 64(3), the cost of 3 books is $192.
For 3.5 books: = 64
(
3.5
)
, the cost of 3.5 books is $224.
We can use the rule that describes the cost function to determine the cost of 3.5 books, but does it make
sense?
No, you cannot buy half of a book.
Is this a discrete rate problem or a continuous rate problem? Explain.
This is a discrete rate problem because you cannot buy a fraction of a book; only a whole number of
books can be purchased.
Example 2 (2 minutes)
This is an example of a continuous rate problem examined in the last lesson.
Let’s revisit a problem that we examined in the last lesson.
Example 2
Water flows from a faucet at a constant rate. That is, the volume of water that flows out of the faucet is the same over
any given time interval. If gallons of water flow from the faucet every minutes, determine the rule that describes the
volume function of the faucet.
Scaffolding:
The definition of discrete is
individually separate or
distinct. Knowing this can help
students understand why we
call certain rates discrete rates.

Lesson 4: More Examples of Functions
Date:
12/18/13
47
© 2013 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
NYS COMMON CORE MATHEMATICS CURRICULUM
8•5
Lesson 4
We said then that the rule that describes the volume function of the faucet is = 3.5, where is the volume
of water in gallons that flows from the faucet and is the number of minutes the faucet is on.
What limitations are there on and ?
Both and should be positive numbers because they represent time and volume.
Would this rate be considered discrete or continuous? Explain.
This rate is continuous because we can assign a number to any positive value of , not just integers.
Example 3 (8 minutes)
This is a more complicated example of a continuous rate problem.
Example 3
You have just been served freshly made soup that is so hot that it cannot be eaten. You measure
the temperature of the soup, and it is °. Since ° is boiling, there is no way it can safely
be eaten yet. One minute after receiving the soup the temperature has dropped to °. If you
assume that the rate at which the soup cools is linear, write a rule that would describe the rate of
cooling of the soup.
The temperature of the soup dropped ° in one minute. Assuming the cooling continues at the
same rate, then if is the number of degrees that the soup drops after minutes pass, = .
We want to know how long it will be before the temperature of the soup is at a
more tolerable temperature of 147°F. The difference in temperature from 210°F to 147°F is 63°F. For what
number will our function assign 63?
63 = 7, then = 9. Our function assigns 63 to 9.
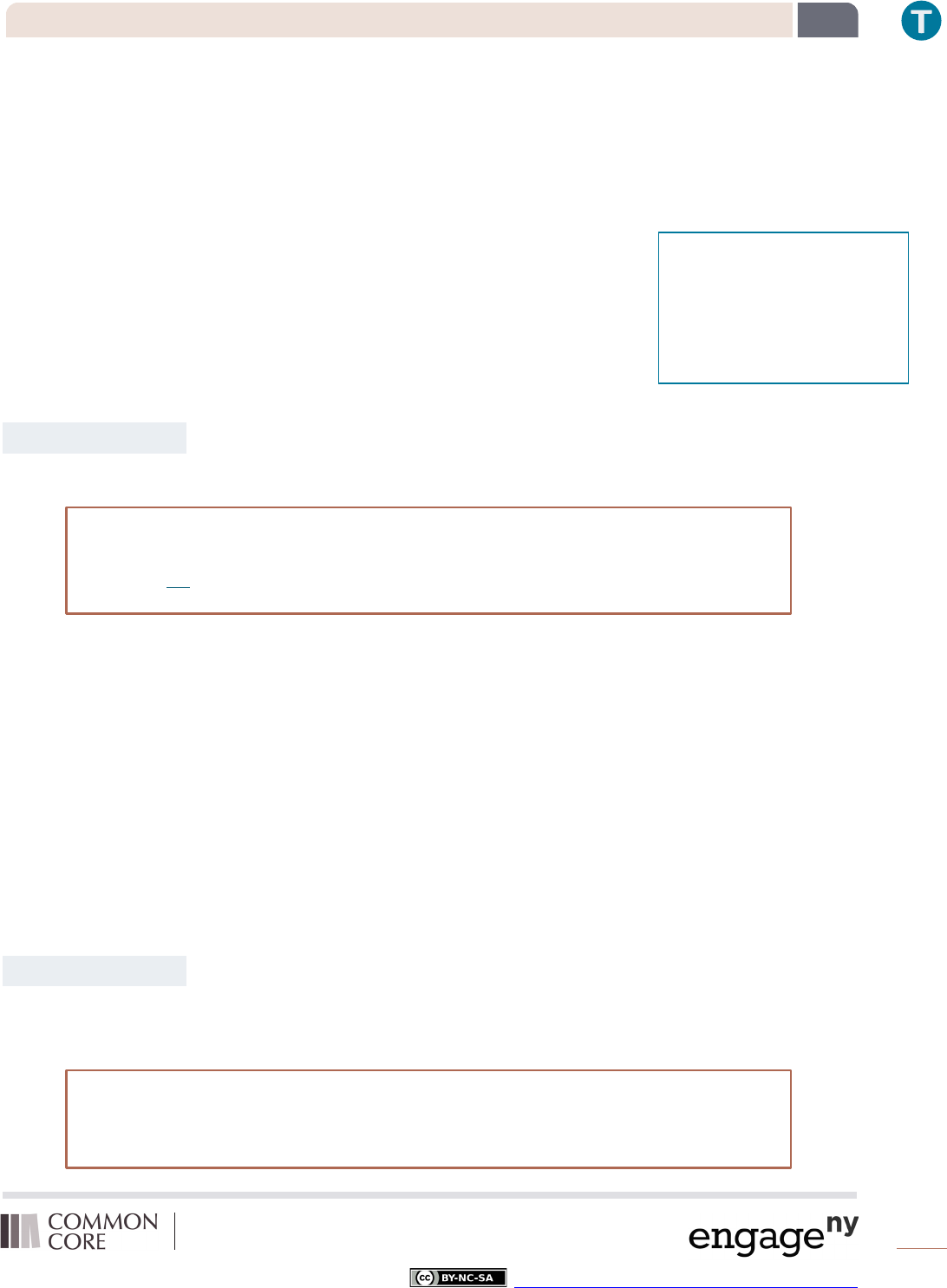
Recall that we assumed that the cooling of the soup would be linear. However, that assumption appears to be
incorrect. The data in the table below shows a much different picture of the cooling soup.
Our function led us to believe that after 9 minutes the soup would be safe to eat. The data in the table shows
that it is still too hot!
What do you notice about the change in temperature from one minute to the next?
For the first few minutes, minute 2 to minute 5, the temperature decreased 6° each minute. From
minute 5 to minute 9, the temperature decreased just 5° each minute.
Scaffolding:
The more real you can make
this, the better. Consider
having a cooling cup of soup,
coffee, or tea with a digital
thermometer available for
students to observe.

Lesson 4: More Examples of Functions
Date:
12/18/13
48
© 2013 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
NYS COMMON CORE MATHEMATICS CURRICULUM
8•5
Lesson 4
Since the rate of cooling at each minute is not linear, then this function is said to be a non-linear function. In
fact, the rule that describes the cooling of the soup is
= 70 + 140
133
140
,
where is the temperature of the soup after minutes.
Finding a rule that describes a function like this one is something you will spend more time on in high school. In
this module, the non-linear functions we work with will be much simpler. The point is that non-linear functions
exist, and in some cases, we cannot think of mathematics as computations of simple numbers. In fact, some
functions cannot be described with numbers at all!
Would this function be described as discrete or continuous? Explain?
This function is continuous because we could find the temperature of the soup for any fractional time
, as opposed to just integer intervals of time.
Example 4 (6 minutes)
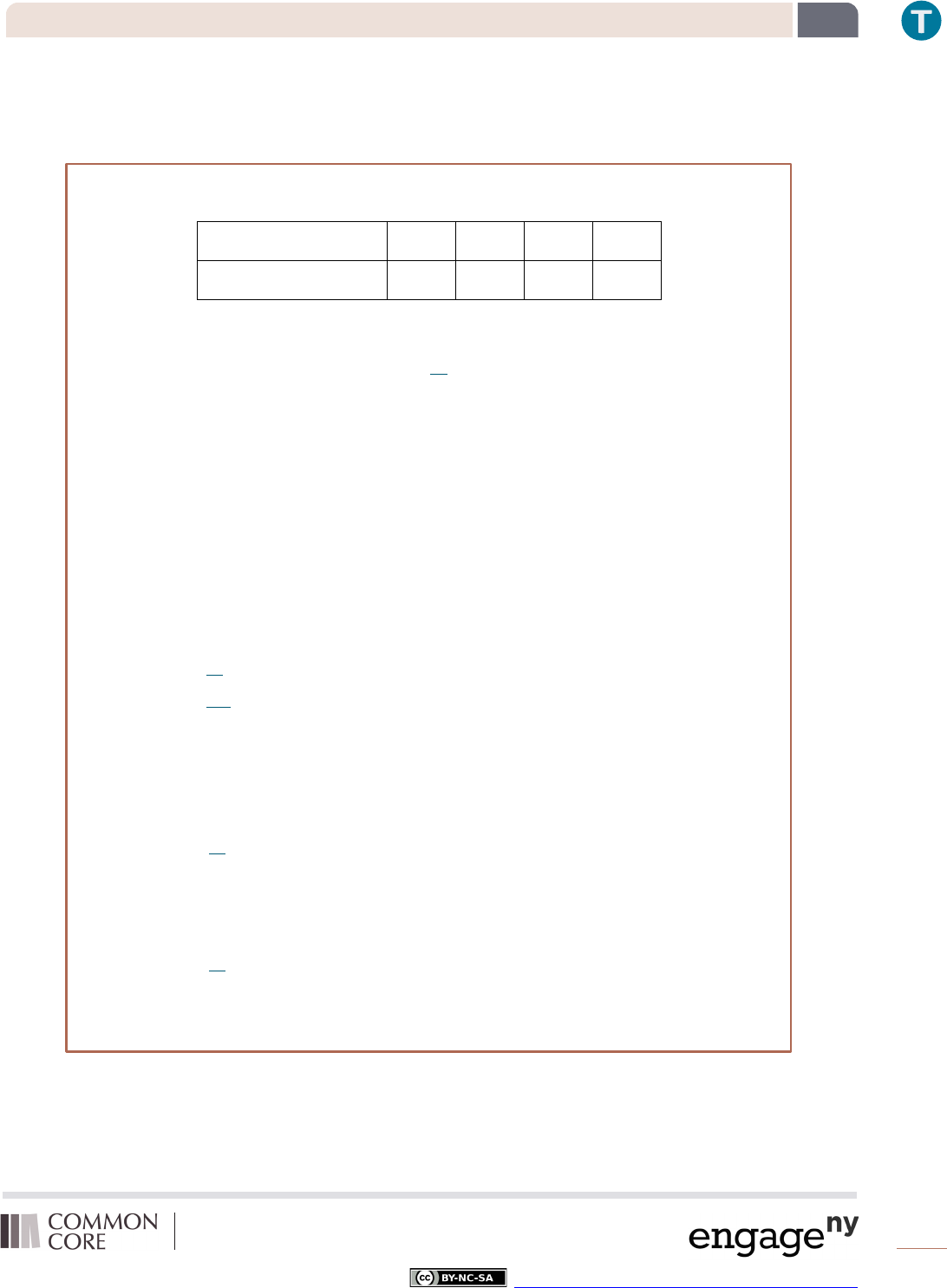
Example 4
Consider the following function: There is a function so that the function assigns to each input, the number of a
particular player, an output, their height. For example, the function assigns to the input, an output of ’”.
’”
’”
’”
’”
’”
’”
’”
’”
’”
The function assigns to the input 2 what output?
The function would assign the height 5’4” to the player 2.
Could the function also assign to the player 2 a second output value of 5’6”? Explain.
No. The function assigns height to a particular player. There is no way that a player can have two
different heights.
Can you think of a way to describe this function using a rule? Of course not. There is no formula for such a
function. The only way to describe the function would be to list the assignments shown in part in the table.
Can we classify this function as discrete or continuous? Explain.
This function would be described as discrete because the input is a particular player and the output is
their height. A person is one height or another, not two heights at the same time.
This function is an example of a function that cannot be described by numbers or symbols, but it is still a
function.
Lesson 4: More Examples of Functions
Date:
12/18/13
49
© 2013 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
NYS COMMON CORE MATHEMATICS CURRICULUM
8•5
Lesson 4
Exercises 1–3 (10 minutes)
Exercises 1–3
1. A linear function has the table of values below related to the number of buses needed for a fieldtrip.
Number of students
(
)
Number of buses
(
)
a. Write the linear function that represents the number of buses needed, , for number of students.
=
b. Describe the limitations of and .
Both and must be positive whole numbers. The symbol represents students, so we cannot have .
students. Similarly, represents the number of buses needed, so we cannot have a fractional number of
buses.
c. Is the rate discrete or continuous?
The rate is discrete.
d. The entire 8
th
grade student body of students is going on a fieldtrip. What number of buses does our
function assign to students? Explain.
=
(
)
=
= . …
.
Ten buses will be needed for the field trip. The function gives us an
assignment of about
.
, which means that
.
buses would be
needed for the field trip, but we need a whole number of buses.
Nine buses means some students will be left behind, so
buses
will be needed to take all
students on the trip.
e. Some 7
th
grade students are going on their own field trip to a different destination, but just are
attending. What number does the function assign to ? How many buses will be needed for the trip?
=
(
)
= . …
.
Six buses will be needed for the field trip.
f. What number does the function assign to ? Explain what this means and what your answer means.
=
(
)
= . …
.
The question is asking us to determine the number of buses needed
for
students. The function assigns, approximately
.
to
.
The function tells us that we need . buses for students, but it
makes more sense to say we need
buses because you cannot
have
.
buses.

Lesson 4: More Examples of Functions
Date:
12/18/13
50
© 2013 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
NYS COMMON CORE MATHEMATICS CURRICULUM
8•5
Lesson 4
2. A linear function has the table of values below related to the cost of movie tickets.
Number of tickets
()
Total cost
(
)
$.
$.
$.
$
a. Write the linear function that represents the total cost,, for tickets purchased.
=
.
= .
b. Is the rate discrete or continuous? Explain.
The rate is discrete. You cannot have half of a movie ticket; therefore, it must be a whole number of tickets
which means it is discrete.
c. What number does the function assign to ? What does the question and your answer mean?
It is asking us to determine the cost of buying tickets. The function assigns to . The answers means that
four tickets will cost $. .
3. A function produces the following table of values.
Input Output
Banana Yellow
Cherry Red
Orange Orange
Tangerine Orange
Strawberry Red
a. Can this function be described by a rule using numbers? Explain.
No, much like the example with the players and their heights, this function cannot be described by numbers or
a rule. There is no number or rule that can define the function.
b. Describe the assignment of the function.
The function assigns to each fruit the color of its skin.
c. State an input and the assignment the function would give to its output.
Answers will vary. Accept an answer that satisfies the function; for example, the function would assign red to
the input of tomato.

Lesson 4: More Examples of Functions
Date:
12/18/13
51
© 2013 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
NYS COMMON CORE MATHEMATICS CURRICULUM
8•5
Lesson 4
Closing (4 minutes)
Summarize, or ask students to summarize, the main points from the lesson:
We know that not all functions are linear and, moreover, not all functions can be described by numbers.
We know that linear functions can have discrete rates and continuous rates.
We know that discrete rates are those where only integer inputs can be used in the function for the inputs to
make sense. An example of this would be purchasing 3 books compared to 3.5 books.
We know that continuous rates are those where we can use any interval, including fractional values, as an
input. An example of this would be determining the distance traveled after 2.5 minutes of walking.
Exit Ticket (4 minutes)
Lesson Summary
Not all functions are linear. In fact, not all functions can be described using numbers.
Linear functions can have discrete rates and continuous rates.
A rate that can have only integer inputs may be used in a function so that it makes sense, and it is then called a
discrete rate. For example, when planning for a field trip, it only makes sense to plan for a whole number of
students and a whole number of buses, not fractional values of either.
Continuous rates are those where any interval, including fractional values, can be used for an input. For example,
determining the distance a person walks for a given time interval. The input, which is time in this case, can be in
minutes or fractions of minutes.
Lesson 4: More Examples of Functions
Date:
12/18/13
52
© 2013 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
NYS COMMON CORE MATHEMATICS CURRICULUM
8•5
Lesson 4
Name Date
Lesson 4: More Examples of Functions
Exit Ticket
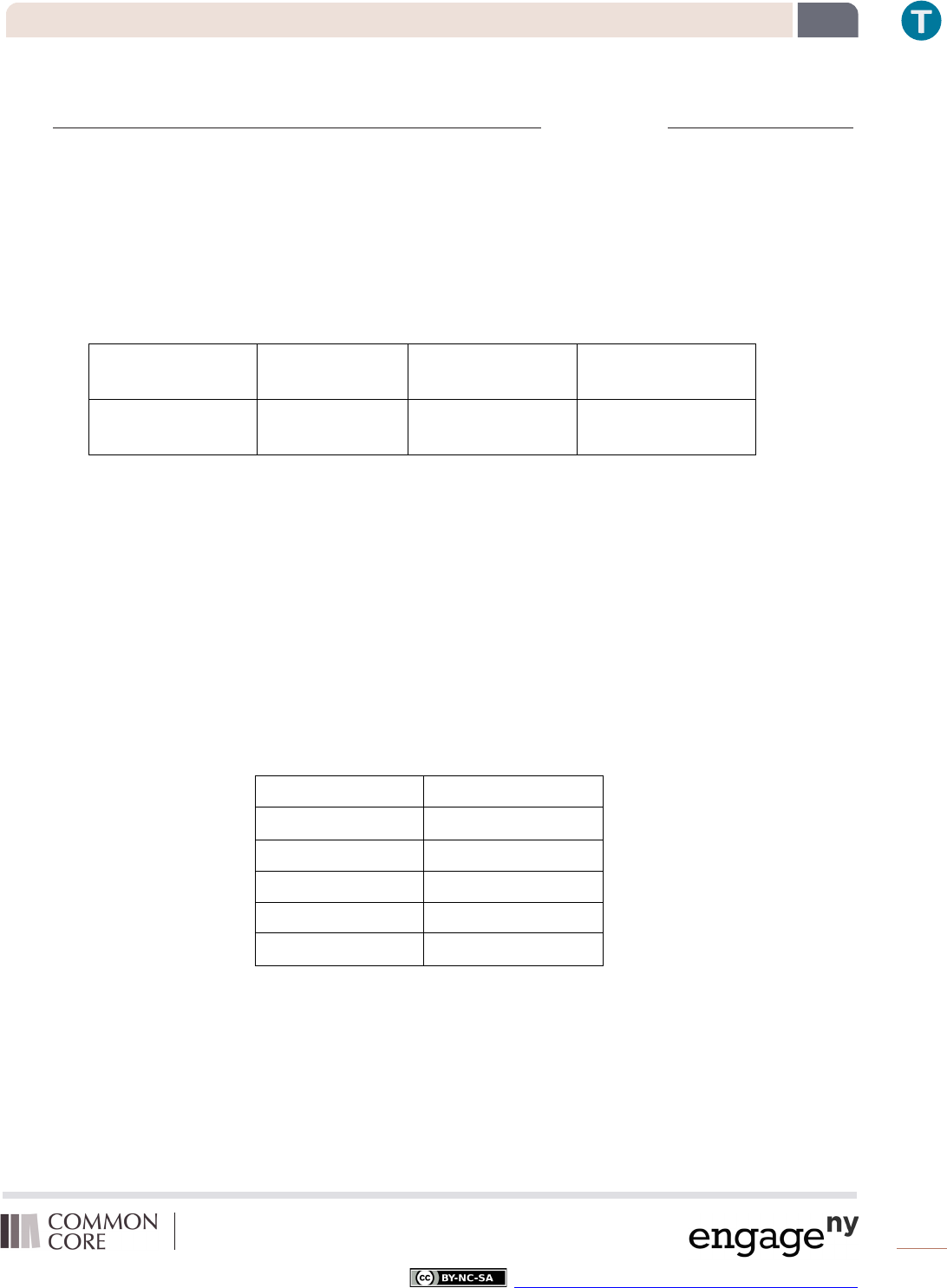
1. A linear function has the table of values below related to the cost of a certain tablet.
Number of tablets
(
)
17
22
25
Total cost
(
)
$10,183
$13,178
$14,975
a. Write the linear function that represents the total cost, , for number of tablets.
b. Is the rate discrete or continuous? Explain.
c. What number does the function assign to 7? Explain.
2. A function produces the following table of values.
Serious Adjective
Student Noun
Work Verb
They Pronoun
And Conjunction
Accurately Adverb
a. Describe the function.
b. What part of speech would the function assign to the word continuous?

Lesson 4: More Examples of Functions
Date:
12/18/13
53
© 2013 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
NYS COMMON CORE MATHEMATICS CURRICULUM
8•5
Lesson 4
Exit Ticket Sample Solutions
1. A linear function has the table of values below related to the cost of a certain tablet.
Number of tablets
(
)
Total cost
(
)
$,
$,
$,
a. Write the linear function that represents the total cost, , for number of tablets.
=
,
=
b. Is the rate discrete or continuous? Explain.
The rate is discrete. You cannot have half of a tablet; therefore, it must be a whole number of tablets which
means it is discrete.
c. What number does the function assign to ? Explain.
The function assigns , to , which means that the cost of tablets would be $, . .
2. A function produces the following table of values.
Serious Adjective
Student Noun
Work Verb
They Pronoun
And Conjunction
Accurately Adverb
a. Describe the function.
The function assigns to each input, a word, the parts of speech.
b. What part of speech would the function assign to the word continuous?
The function would assign the word adjective to the word continuous.
Lesson 4: More Examples of Functions
Date:
12/18/13
54
© 2013 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
NYS COMMON CORE MATHEMATICS CURRICULUM
8•5
Lesson 4
Problem Set Sample Solutions
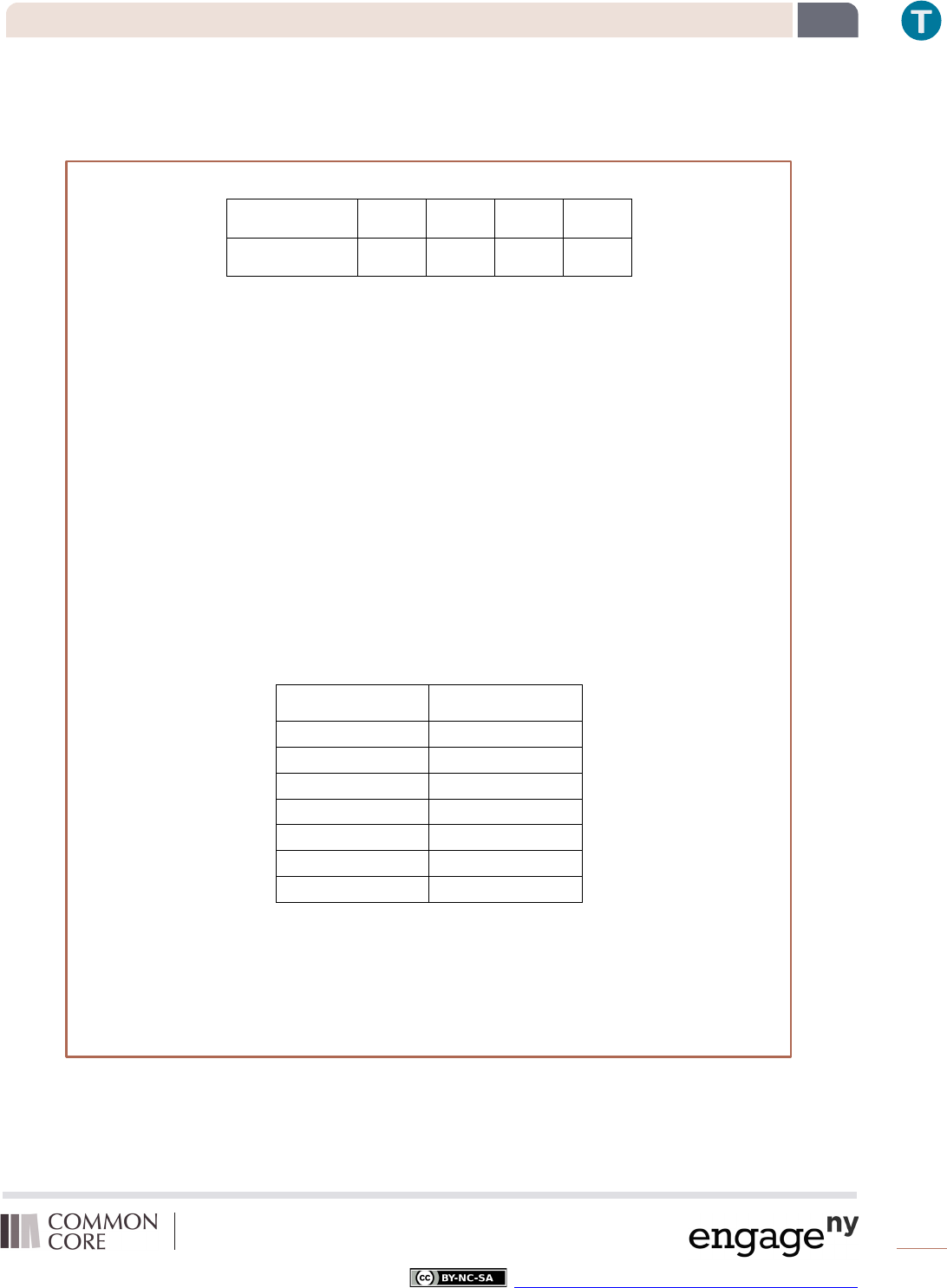
1. A linear function has the table of values below related to the total cost for gallons of gas purchased.
Number of gallons
(
)
.
Total cost
(
)
$.
$.
$.
$.
a. Write the linear function that represents the total cost, , for gallons of gas.
= .
b. Describe the limitations of and .
Both and must be positive rational numbers.
c. Is the rate discrete or continuous?
The rate is continuous.
d. What number does the function assign to ? Explain what your answer means.
= . ()
=
The function assigns to . It means that if gallons of gas are purchased, it will cost $.
2. A function has the table of values below. Examine the information in the table to answer the questions below.
Input Output
one
two
three
four
five
six
seven
a. Describe the function.
The function assigns to each input, a word, the number of letters in the word.
b. What number would the function assign to the word “eleven”?
The function would assign the number to the word eleven.

Lesson 4: More Examples of Functions
Date:
12/18/13
55
© 2013 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
NYS COMMON CORE MATHEMATICS CURRICULUM
8•5
Lesson 4
3. A linear function has the table of values below related to the total number of miles driven in a given time interval in
hours.
Number of hours driven
(
)
Total miles driven
(
)
a. Write the linear function that represents the total miles driven, , for number of hours.
=
=
b. Describe the limitations of and .
Both and must be positive rational numbers.
c. Is the rate discrete or continuous?
The rate is continuous.
d. What number does the function assign to ? Explain what your answer means.
=
(
)
=
The function assigns to . The answer means that miles are driven in hours.
e. Use the function to determine how much time it would take to drive miles.
=
=
. … =
.
It would take about . hours to drive miles.
4. A function has the table of values below that gives temperatures at specific times over a period of hours.
12:00 p.m.
°
1:00 p.m.
. °
2:00 p.m.
°
4:00 p.m.
°
8:00 p.m.
°
a. Is the function a linear function? Explain.
Yes, it is a linear function. The change in temperature is the same over each time interval. For example, the
temperature drops . ° from 12:00–1:00 and 1:00–2:00. The temperature drops ° from 2:00–4:00, which is
the same as . ° each hour and ° over a four hour period of time, which is also . ° per hour.

Lesson 4: More Examples of Functions
Date:
12/18/13
56
© 2013 Common Core, Inc. Some rights reserved. commoncore.org
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
NYS COMMON CORE MATHEMATICS CURRICULUM
8•5
Lesson 4
b. Describe the limitations of and .
The input is a particular time of the day and is the temperature. The input cannot be negative, but could be
intervals that are fractions of an hour. The output could potentially be negative because it can get that cold.
c. Is the rate discrete or continuous?
The rate is continuous. The input can be any interval of time, including fractional amounts.
d. Let represent the temperature and represent the number of hours from 12:00 p.m. Write a rule that
describes the function of time on temperature.
= .
e. Check that the rule you wrote to describe the function works for each of the input and output values given in
the table.
At 12:00, hours have passed since 12:00, then = .
(
)
= .
At 1:00, hour has passed since 12:00, then = .
(
)
= . .
At 2:00, hours have passed since 12:00, then = .
(
)
= .
At 4:00, hours have passed since 12:00, then = .
(
)
= .
At 8:00, hours have passed since 12:00, then = .
(
)
= .
f. Use the function to determine the temperature at 5:30 pm.
At 5:30, . hours have passed since 12:00, then = .
(
.
)
= . .
The temperature at 5:30 will be . °.
g. Is it reasonable to assume that this function could be used to predict the temperature for 10:00 a.m. the
following day or a temperature at any time on a day next week? Give specific examples in your explanation.
No, the function can only predict the temperature for as long as the temperature is decreasing. At some point
the temperature will rise. For example, if we tried to predict the temperature for a week from 12:00 p.m.
when the data was first collected, we would have to use the function to determine what number it assigns to
because would be the number of hours that pass in the week. Then we would have
= .
(
)
=
which is an unreasonable prediction for the temperature.
